Biot-Savart law and application is most important topic of NCERT Magnetic effect of current chapter in Class 12th. Questions are frequently asked in the CBSE board and ICSE Board exam from Biot-savart law .
“physics – Application of Biot- savart law 12th notes “ will be very beneficial for the
students who are engaged in the preparation of
upcoming board exam, JEE IIT , NEET , AIMS, State engineering entrance exam .
In this topic, the following terms will be illustrated.
Contents :
* 1.1 Magnetic Field Pattern due to Straight
Current-Carrying Conductor
* 1.2. Maxwell's right- hand thumb rule
* 1.3 - Maxwell's corkscrew rule
* 2.1 Magnetic field density due to current carrying straight conductor
of finite length
* 2.2. Magnetic field density due to current carrying straight conductor
of infinite length
* 3.1. Magnetie Field Pattern due to a Circular Loop Current Carrying conductor
* 3.2. Direction of magnetic field at any point on the axis of circular coil
* 3.3. Magnetic field at the centre of current carrying circular
coil
* 3.4. Magnetic field on the axis of current carrying coil
1.1. Magnetic Field Pattern due to Straight
Current-Carrying Conductor:
* The magnetic field lines around a straight current
carrying conductor are concentric circles whose centers lie on the conductor.
* When current in the wire flows in the upward direction
then the lines of magnetic field are in the anticlockwise direction.
* When current in the wire flows in the downward direction then the lines of magnetic field are in the clockwise direction
* Direction of magnetic field produced by a straight
current- carrying conductor can be known
by Maxwell right hand rules.
1.2 - Maxwell's right- hand thumb rule
 |
| Maxwell's right hand thumb rule |
According to Maxwell's right- hand thumb rule :
grasp the current-carrying
conductor in right hand so that thumb points in the direction of current,
then the direction in which fingers
encircle the conductor will give the
direction of magnetic field lines around the conductor .
1.3 - Maxwell's corkscrew rule
Imagine driving a corkscrew in the direction of
current, then the direction in which we turn its handle is the direction of
magnetic field.
2.1. Magnetic field due to current carrying straight conductor of finite length :
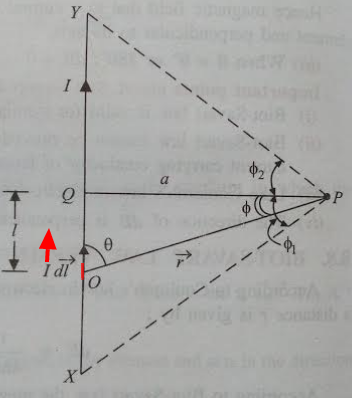 |
| Magnetic field due to current carrying conductor |
* Consider a current carrying straight conductor XY lying in
the plane of the paper
* Let Direction of current be from X to Y
* We have to find magnetic field at point P located at
perpendicular distance ‘ a ‘ from conductor.
i.e PQ = a
* Point P is
situated such that ,
Angle between PQ and PX
= ϕ1
Angle between PQ and PY = ϕ2
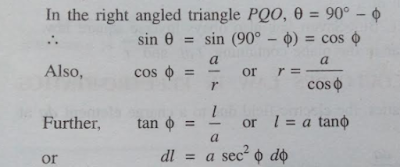 |
| Putting the value of sinθ , dl , and r in eq ( i ) , we have |
* since each small segment of conductor contribute to the magnetic field in
same direction , then total magnetic
field at point P is obtained by using integration over the length XY .
 |
* Thus , magnetic field at point P located at perpendicular distance R is |
2.2. Magnetic field due to current carrying straight conductor of infinite length :
(a ) . If point P is near the center of conductor
In this case ,
Φ1 = 900
and Φ2
= 900 = π / 2
So ,
(b ) . If point P is near the one end ( X) of conductor
In this case ,
Φ1 = 00 and Φ2 = 900 = π / 2 and
perpendicular distance = R
3.1. Magnetie Field Pattern due to a Circular Loop (or Circular Wire) Current Carrying conductor :
* When a current is passed through the circular loop of wire, magnetic field is produced around it.
* The magnetic field lines are circular near the
current-carrying loop.
* As we move toward centre of circular loop the concentric circles representing magnetic
field lines become bigger and bigger.
* At the centre of the circular loop, the magnetic field lines
are nearly straight .
* Each segment of circular loop carrying current produces
magnetic field lines in the same direction near the centre of loop.
* At the centre of the circular loop, all the magnetic field
lines are in the same direction and aid each other, due to which the strength
of magnetic field increases .
3.2. Direction of magnetic field at any point on the axis of circular coil
Right hand fist rule
According to this rule, hold the axis of the coil in the right hand fist in such a way that fingers point in the direction of current in the coil. Then outstretched thumb gives the direction of magnetic field at any point on the axis of coil.
3.3. Magnetic field density at the centre of current
carrying circular coil
* Let radius of current carrying circular coil be
r
* Suppose the loop lies in the plane of paper
* when current flow in coil in clockwise
direction , then magnetic field is
produced at the center of coil in
downward direction of plane .
* we have to find magnetic field at the center
Magnetic field at center due to small segment
of coil is dB.
For each current element , the angle between dl and r is 90
so,
Net magnetic field at the center of coil ,
If the coil has N turns, then net magnetic field at center
B = μ0 N I / 2r
.
3.4. Magnetic Field density on the axis of current carrying circular coil
* Let radius of current carrying circular coil be r having center ‘ O ‘ and
plane of coil is perpendicular to
the plane of horizontal surface .
Now , We have to calculate magnetic field at point P on the axis of coil
such that OP = x
Calculation :
* Consider two small current segments of coil Q and
R having length dl are located diametrically
opposite to each other and Distance of
each segment from point P = r
Ie. PQ = PR = r
Angle between dl and r is 900
.
Let magnitude of magnetic field at point P due to
current segment Q and R are dB
and dB’ respectively ,
According to Biot Savart law
and ,
Resolving dB
and dB’ into rectangular components .
* Vertical components ( dB cosα and dB' cosα) cancel each other because both components are equal and opposite .
* Components along the axis of coil are added and act in direction PX.
* This is true for all the diametrically opposite
segments of coil.
Hence the resultant magnetic field at point P is the
sum of all horizontal components
Next Topic : Ampere's Circutials Law and its Applications
If you liked the notes of application of Biot
Savart law, then share it with other students.
If you want to ask any question related to topic law
of Biot- Savart and then
write a question in the comment box.














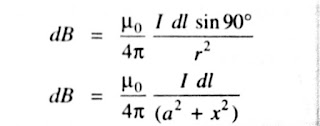



No comments:
Post a Comment